알고리즘으로 생각하기 - 양성봉 참고
백준 문제를 풀다가 알고리즘 풀이가 잘 기억이 나지 않아서
교과서에 있는 알고리즘 코드를 외우기 위해 작성
선택 정렬
설명
해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 그 위치에 어떤 원소를 넣을지 선택하는 알고리즘
시간 복잡도
O(n^2)

알고리즘
[1] 주어진 배열 중에 최소값을 찾는다.
[2] 그 값을 맨 앞에 위치한 값과 교체한다. (pass)
[3] 맨 처음 위치를 뺀 나머지 배열을 같은 방법으로 교체한다.
[4] 하나의 원소만 남을 때까지 위의 1~3 과정을 반복한다.
코드
def selection_sort(arr):
for i in range(len(arr) - 1):
min_idx = i
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
버블 정렬
설명
서로 인접한 두 원소를 검사하여 정렬하는 알고리즘.
시간 복잡도
O(n^2)
알고리즘
인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다.
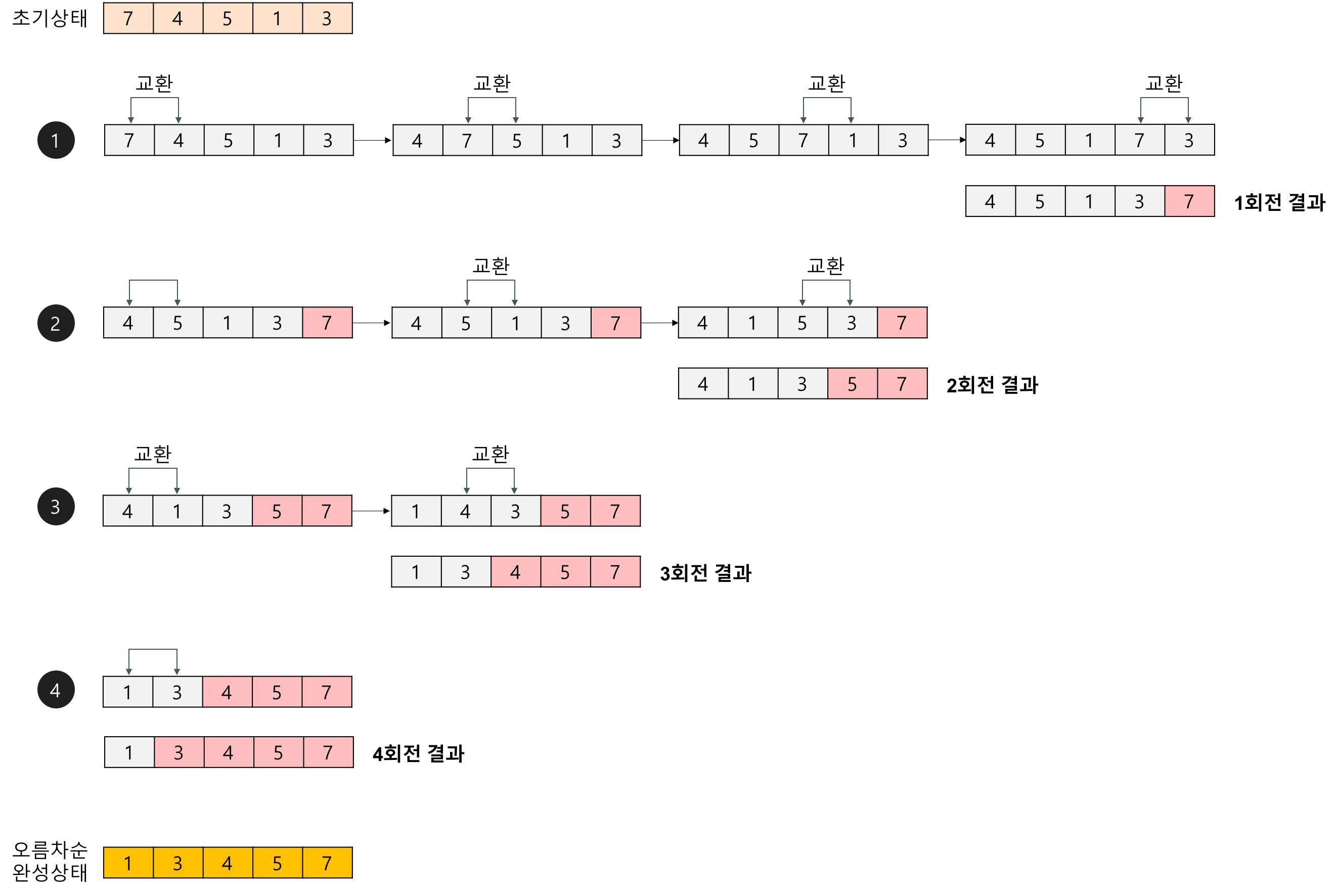
코드
def bubble_sort(arr):
for i in range(len(arr) - 1, 0, -1):
for j in range(i):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
input_list = [50, 80, 75, 30, 95, 90, 45, 10, 15, 70, 85, 30, 20, 50, 60, 20]
print('정렬 전:\t', input_list)
bubble_sort(input_list)
print('정렬 후:\t', input_list)
코드 설명
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
단순하게 arr의 앞 숫자와 뒷 숫자를 비교해서 교환하는 코드인데,
이중 for문을 사용해 n회전을 하며 정렬한다.
파티션 (partition) 함수
def partition(a, pivot, high):
i = pivot + 1
j = high
while True:
while i < high and a[i] <= a[pivot]:
i += 1
while j > pivot and a[j] > a[pivot]:
j -= 1
if j <= i:
break
a[i], a[j] = a[j], a[i]
j += 1
j -= 1
a[pivot], a[j] = a[j], a[pivot]
return j
피벗을 기준으로 피벗보다 작으면 왼쪽, 크면 오른쪽으로 분할하는 partition 함수 (정렬은 X)
퀵 정렬 (partition 함수 사용)
설명
입력의 맨 왼쪽 원소(피벗)를 기준으로 피벗과 같거나 작은 원소들과 큰 원소들을 각각 피벗의
좌우로 분할한 후, 분할된 부분들을 각각 같은 방법으로 정렬하는 알고리즘
시간 복잡도
최선 O(nlogn), 최악 O(n^2)

알고리즘
[1] 맨 왼쪽 숫자를 피벗으로 삼는다.
[2] 피벗과 각 숫자를 비교하여 피벗보다 작거나 같은 숫자들은 왼쪽으로 큰 숫자들은 피벗을 그사이로 옮긴다.
[3] 피벗보다 작거나 오른쪽으로 나누고, 같은부분을 동일한 방법으로 정렬한다.
[4] 피벗보다 큰 부분을 동일한 방법으로 정렬한다.
코드
def qsort(a, low, high):
if low < high:
pivot = partition(a, low, high)
qsort(a, low, pivot - 1)
qsort(a, pivot + 1, high)
input_list = [50, 80, 75, 30, 95, 90, 45, 10, 15, 70, 85, 30, 20, 50, 60, 20]
print('정렬 전:\t', input_list)
qsort(input_list, 0, len(input_list) -1)
print('정렬 후:\t', input_list)
피벗을 활용해 오름차순 정렬
합병 정렬
설명
데이터 개수가 1개가 될 때까지 계속 분할
시간 복잡도
어떤 상황에서도 O(nlogn)

합병 정렬(Merge Sort)은 크기가 n인 입력을 1/2n 크기 2개로 분할하고,
각각에 대해 같은 방법으로 합병 정렬을 수행한 후 2개의 각각 정렬된 부분을 합병
합병(Merge): 2개의 각각 정렬된 리스트를 합치어 정렬하는 것
알고리즘
[1] 현재 입력 크기가 1이면 return
[2] 현재 입력을 반으로나눈다.
[3] 앞부분을 동일한 방법으로 정렬한다.
[4] 뒷부분을 동일한 방법으로 정렬한다.
[5] 정렬된 앞부분과 뒷부분을 합병한다.
코드
def merge(a, b, low, mid, high):
i = low
j = mid + 1
for k in range(low, high + 1): # a의 앞/뒷부분을 합병하여 b에 저장
if i > mid:
b[k] = a[j] # 앞부분이 먼저 소진된 경우
j += 1
elif j > high:
b[k] = a[i] # 뒷부분이 먼저 소진된 경우
i += 1
elif a[j] < a[i]:
b[k] = a[j] # a[j]가 승자
j += 1
else:
b[k] = a[i] # a[i]가 승자
i += 1
for k in range(low, high + 1):
a[k] = b[k] # b를 a에 복사
def merge_sort(a, b, low, high):
if high <= low:
return
mid = low + (high - low) // 2
merge_sort(a, b, low, mid) # 왼쪽 부분 순환 호출
merge_sort(a, b, mid + 1, high) # 오른쪽 부분 순환 호출
merge(a, b, low, mid, high) # 왼쪽과 오른쪽 부분 합병
input_list = [37, 10, 22, 30, 35, 13, 25, 24]
aux = [None] * len(input_list) # 보조 리스트
print('정렬 전:\t', input_list)
merge_sort(input_list, aux, 0, len(input_list) - 1) # 합병 정렬 호출
print('정렬 후:\t', input_list)
크기가 1이 될 때까지 분할 -> 전체 정렬 될 때까지 합병
k 번째 작은 수
설명
피벗을 사용해 K번째 작은 수를 구하는 알고리즘
k를 수정하여 < 피벗보다 큰 쪽일 때 k를 수정하여 k-p로 가야 될 수도 있지만
배열을 건드리지 않으면 그대로 k 수정 없이 가도 된다.
시간 복잡도
피벗을 사용. O(n)
최악은 O(nlogn)이지만 평균적으로 O(n)
알고리즘
[1] 피벗을 랜덤하게 선택한다.
[2] 피벗과 각 숫자를 비교하여 피벗보다 작은 숫자들을 왼쪽으로, 큰 숫자들을 오른쪽으로나누고, 피벗을 그사이에 둔다.
[3] K번째 작은숫자가 피벗이면 탐색 성공
[4] K번째 작은 숫자가 피벗보다 작은부분에 있으면,작은 부분에서 동일한 방법으로 탐색
[5] 피벗보다 큰 부분에 있으면, K를 수정하여 큰 부분에서 동일한 방법으로 탐색
코드
def partition(a, pivot, high):
i = pivot + 1
j = high
while True:
while i < high and a[i] < a[pivot]:
i += 1
while j > pivot and a[j] > a[pivot]:
j -= 1
if j <= i:
break
a[i], a[j] = a[j], a[i]
i += 1
j -= 1
a[pivot], a[j] = a[j], a[pivot]
return j
def selection(a, low, high, k):
pivot = partition(a, low, high)
if k < pivot:
return selection(a, low, pivot-1, k)
elif k == pivot:
return a[k]
else:
return selection(a, pivot+1, high, k)
input_list = [40, 20, 50, 70, 65, 90, 35, 10, 15, 60, 55, 80, 25, 75]
K = input('(k-1) 값을 입력하라(0부터 ' + str((len(input_list)-1)) + '): ')
kth_smallest = selection(input_list, 0, len(input_list)-1, int(K))
print('{:2}번째 작은 수는 {:2}이다.'.format(int(K)+1, kth_smallest))



