4. 작은 것부터 풀어보기 (DP)

알고리즘으로 생각하기 - 양성봉 참고

 

백준 문제를 풀다가 알고리즘 풀이가 잘 기억이 나지 않아서

교과서에 있는 알고리즘 코드를 외우기 위해 작성

 

작은 것부터 풀어보기

설명

문제를 작은 것부터 풀어본다 → 작은 문제들을 먼저 풀어서 그 해를 이용하여 문제 해결

→ 동적 계획

 

작은 문제: 원래 주어진 문제와 같은 문제, 작은 문제를 부분 문제라고 함

 

가장 긴 증가 순서

설명

숫자가 일렬로 나열되었을 때 가장 긴 증가 순서를 찾아보자.

증가 순서는 숫자들이 반드시 이웃해야만 할 필요 X

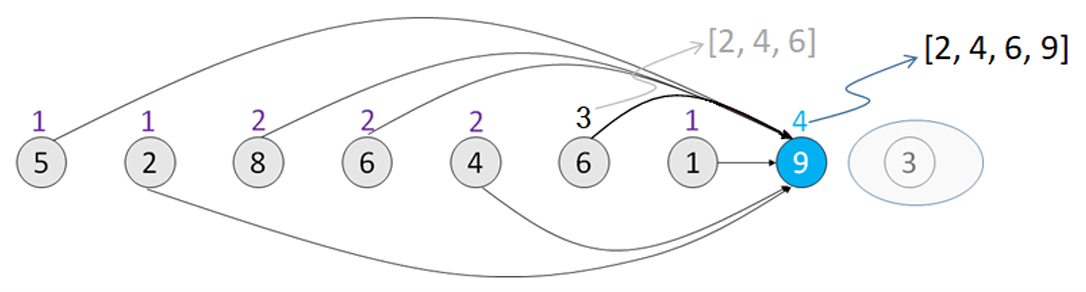
[5, 2, 8, 6, 4, 6, 1, 9, 3]에서 [5, 8, 9], [5, 6, 9], [2, 4, 6, 9] 등 전부 증가 순서

가장 긴 증가 순서는 [2, 4, 6, 9]이다.

 

문제를 다른 형태의 문제로 바꾸어 생각하기 → 그래프 만들기

각 점에서 오른쪽에 위치한 점에 대해서 자신보다 큰 숫자를 가진 점을 간선으로 연결

가장 긴 증가 순서는 그래프에서 가장 긴 경로에 있는 숫자들과 같다.

 

알고리즘

[1] 주어진 숫자들을 가지고 그래프를 만듦

[2] 가장 왼쪽 정점으로부터 하나씩 차례로 각 정점으로 들어오는 간선의 왼쪽 끝 정점까지

[3] 계산된 경로의 길이들 중에서 가장 긴 것에 1을 더하여 (끝 정점 +1) 경로의 길이를 계산

[4] 각 점의 경로 길이 중에서 가장 긴 것을 리턴한다.

 

 

시간 복잡도

그래프 만드는데 n(n-1)/2

좌에서 우로 들어오는 간선에 대한 연산량 = 그래프의 간선 수

알고리즘의 수행 시간 O(n^2)

 

코드

s = [5, 2, 8, 6, 4, 6, 1, 9, 3]  # 입력 순서

n = len(s)  # 그래프 정점 수

g = [None, None, [0, 1], [0, 1], [1], [0, 1, 4], None, [0, 1, 2, 3, 4, 5, 6], [1]]

previous = [-1 for _ in range(n)]  # 순서 추출을 위해

length = [1 for _ in range(n)]     # 길이 초기화

for i in range(1, n):

    if g[i] is not None:

        max_length = -1

        for j in g[i]:  # 들어오는 간선의 각 끝점 j에 대해

            if length[j] > max_length:

                max_length = length[j]

                previous[i] = j

        length[i] = max_length + 1

print('가장 긴 증가 순서의 길이 =', max(length))

k = length.index(max(length))  # k는 가장 긴 길이를 가진 항목의 인덱스

seq = [k]  # 순서 역추적

while previous[k] != -1:

    seq.insert(0, previous[k])

    k = previous[k]

lis = [s[i] for i in seq ]

print('가장 긴 증가 순서 = ', lis)

 

Bellman-Ford 최단 거리 알고리즘

설명

다익스트라 최단 경로 알고리즘의 문제점:

이미 확정된 점들에 대한 간선 완화를 수행하지 않음, 그리디 알고리즘은

한번 선택하여 확정된 값에 대해 수정을 허락하지 않기 때문

 

음수 사이클: 사이클 상의 간선의 가중치의 합이 음수인 사이클

 

반복할수록 거리 짧아져서 최단 경로 찾는 문제 성립 X

따라서 최단 경로 찾는 알고리즘에 음수 사이클은 존재 X

 

선형 그래프의 출발점부터 시작해서 좌에서 우로 간선 완화를 단계적으로 수행

일괄 처리 수행, 간선 완화 1회 시도할 때마다 모든 점이 간선 완화 시도에 참여

 

Bellman-Ford 알고리즘이 작은 것부터 풀어보기 방식인 이유:

그래프는 한눈에 부분 문제 확인하기 어렵지만 시작점이 가장 작은 문제

직전 점까지의 해를 찾은 후 그 다음 최단 경로가 확정되기 때문

 

알고리즘

<i, j> i부터 j까지 라는 뜻

D[j]가 저거보다 더 크다면, 더 작아질 수 있으므로

D[j]를 D[i] + 간선 <i, j>의 가중치로 바꿔서 간선 완화

 

반복하면서 업데이트 함(간선 완화), 왼쪽에서 오른쪽으로 n-1회 수행

 

시간 복잡도

각 간선에 대해 n-1회 간선 완화 수행

간선 수가 m이면 수행 시간은 O(mn)

그래프를 인접 행렬로 사용하면 O(n^2)

 

코드

INF = float('inf')

graph = [[INF, 3, 4, INF, INF, INF, INF],

         [INF, INF, INF, 1, INF, INF, INF],

         [INF, INF, INF, INF, 2, INF, INF],

         [INF, INF, INF, INF, 4, -1, INF],

         [INF, -4, INF, INF, INF, INF, 3],

         [INF, INF, INF, INF, INF, INF, 1],

         [INF, INF, INF, INF, INF, INF, INF]]

n = len(graph)  # 그래프 정점의 수

s = 0  # 출발점

D = [INF for _ in range(n)]

D[s] = 0

previous = [-1 for _ in range(n)]

previous[s] = 0

#for k in range(n - 1):  # n-1회 반복

for k in range(n):  # n회 반복시 relaxation 없으면 음의 순환 사이클 없음

    print('%d 번째 완화 시도' % k)  #추가

    for i in range(n):

        for j in range(n):

            if graph[i][j] != INF:

                if D[j] > D[i] + graph[i][j]:

                    D[j] = D[i] + graph[i][j]  # 간선 완화

                    previous[j] = i  # i 덕분에 j까지 거리가 단축됨

                    print('relaxation is done with previous[%d] = %d' % (j, i)) #추가

# 결과 출력

print('정점 %1d으로부터의 최단 거리' % s)

for i in range(n):

    print('[%d, %d] = %3d' % (s, i, D[i]))

print()

print('정점 0으로부터의 최단 경로')

for i in range(n):

    back = i

    print(back, end='')

    while back != 0:

        print(' <-', previous[back], end='')

        back = previous[back]

    print()

 

서열 정렬

 

설명

어느 DNA가 다른 DNA로 변형되는데 얼마나 많은 변이가 필요한가 계산하는 문제

변이는 삽입, 삭제, 대체의 연산

 

ex) 문서 편집기: 스트링 S를 수정하여 스트링 T로 변환시킬 때 사용

편집 거리를 최소화하는 문제: (편집 거리: S를 T로 변환시키는데 최소 편집 연산 횟수)

앞부분에서 최적을 발견한 상태에서 뒷부분 해결

 

부분 문제 E[i, j] = S의 접두부(맨 앞)의 i개 문자를 T의 접두부 j개 문자로 변환시키는 데 필요한

최소 연산 횟수

 

E[i, j] 연산 방법: 세 방향에서 계산하는데 이 중 가장 작은 min값을 계산함.

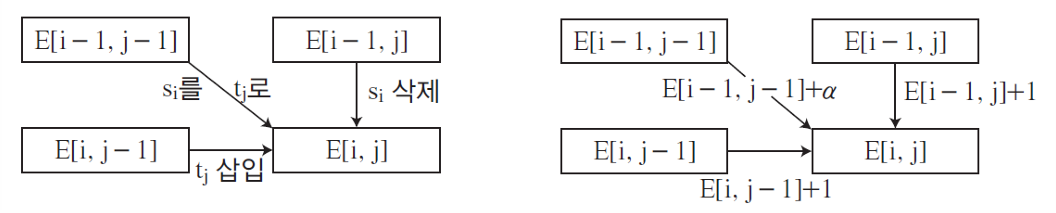
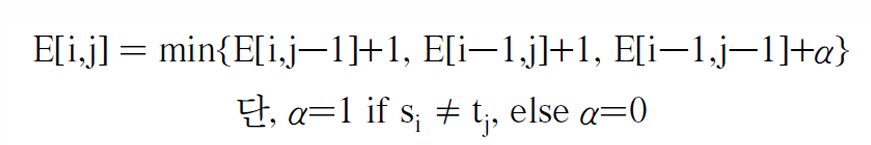
단, 부분 -> si와 tj가 다르면 대체연산 1, 같으면 그대로니까 0

 

알고리즘

2차원 mn (ST) 리스트 E를 첫 번째 행부터 차례로 각 원소에 주변 3개의 해로

계산된 결과 중에서 최솟값을 저장한다.

return E[m, n]

 

위쪽에서 오면 삭제, 왼쪽에서 오면 삽입, 대각선에서 오면 대체orX변화

 

시간 복잡도

O(m*n)

 

코드

S = 'script'

T = 'scope'

m = len(S)

n = len(T)

E = [[_ for _ in range(n+1)] for _ in range(m+1)]

for i in range(m+1):

    E[i][0] = i

for j in range(n+1):

    E[0][j] = j

for j in range(1, n + 1):

    for i in range(1, m + 1):

        if S[i - 1] == T[j - 1]:  # S의 i-1번째 문자와 T의 j-1번째 문자

            alpha = 0

        else:

            alpha = 1

        E[i][j] = min(E[i - 1][j] + 1,

                      E[i][j - 1] + 1,

                      E[i - 1][j - 1] + alpha)

print(S, '->', T, '의 편집 거리:', E[m][n])

#S = 'kitten'

#T = 'sitting'